1.(2005?盐城三模)为了探索弹力和弹簧伸长的关系,李卫同学选了甲、乙两根规格不同的弹簧进行测试,根据
2.(2012?盐城三模)小球藻是一种单细胞藻类,常作为生物学研究的材料.(1)以下是用不同辐射剂量的紫外线
3.(2012?盐城三模)如图所示,光滑绝缘水平桌面上有A、B两个带电小球(可以看成点电荷),A球带电量为+2q
4.(2013?盐城三模)如图,三棱锥P-ABC中,已知PA⊥平面ABC,△ABC是边长为2的正三角形,D,E分别为PB,PC
5.(2014?盐城三模)如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为菱形,点F为侧棱PC上一点.(1)若PF=
6.(2013?盐城三模)如图,一颗棋子从三棱柱的一个顶点沿棱移到相邻的另一个顶点的概率均为13,刚开始时,
7.(2013?盐城三模)如图是7位评委给某作品打出的分数的茎叶图,那么这组数据的方差是______
解答:证明:连接OC、OE,则∠COE=2∠CDE
∵
=
,∴∠AOC=∠AOE
∴∠AOC=∠CDE
∴∠COP=∠PDF
∵∠P=∠P
∴△PDF∽△POC
∴
=
∴PF×PO=PD×PC
由割线定理可得PC×PD=PA×PB
∴PF?PO=PA?PB.
(2005?盐城三模)为了探索弹力和弹簧伸长的关系,李卫同学选了甲、乙两根规格不同的弹簧进行测试,根据
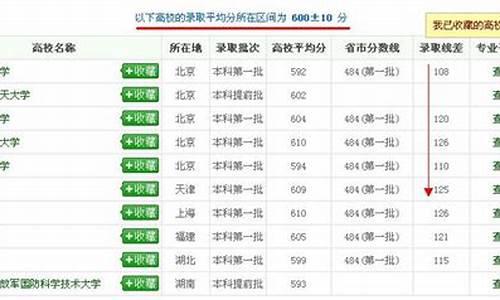
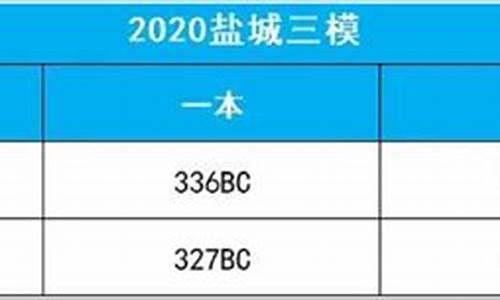
物理类本一线:508。本二线444。历史类本一线:536。本二线473。
此次模考总计有31092人参加,均分最高的是盐都区,最低的是响水县,大丰区和东台市不相上下,盐都区则遥遥领先。
(2012?盐城三模)小球藻是一种单细胞藻类,常作为生物学研究的材料.(1)以下是用不同辐射剂量的紫外线
根据胡克定律,在弹性限度内,弹簧的弹力与行变量成正比,故F-x图是直线,向上弯曲的原因是超出了弹性限度,注意该图象中纵坐标为伸长量,横坐标为拉力,斜率的倒数为劲度系数,由此可求出kA=66.7N/m,kB=200N/m,由于A的劲度系数小,因此其精度高.
故答案为:超过弹簧的弹性限度,66.7,200,A.
(2012?盐城三模)如图所示,光滑绝缘水平桌面上有A、B两个带电小球(可以看成点电荷),A球带电量为+2q
(1)①根据题意和图表分析可知:在对小球藻的相对含量进行计数之前不需要对样品进行稀释;当所用的UV-B辐射剂量为0.8J/m2,小球藻的相对含量在增加;当所用的UV-B辐射剂量为1.6J/m2,小球藻的相对含量开始减少,所以能抑制小球藻生长的最小剂量是1.6J/m2.进行实验时,为减小实验数据误差,要进行重复实验(或重复计数)并计算平均值.
②在生态系统的能量流动中,生产者固定的太阳能总量就是流经该生态系统的总能量.因此,UV-B辐射剂量增高导致生产者(或海藻)数量减少,生产者固定的能量减少,流入各营养级的能量减少,最终导致海洋生物总量减少.
(2)根据题意和图示分析可知:酵母菌无氧呼吸能产生C02,乳酸菌无氧呼吸不产生C02.所以置于相同适宜的光照条件下进行实验.小球藻光合速率较快的是B试管.
D瓶中发生的呼吸作用产物是乳酸,反应式为.
答案:(1)①不需要 ?1.6 J/m2? 进行重复实验(或重复计数)并计算平均值
②生产者(或海藻)数量减少,生产者固定的能量减少,流入各营养级的能量减少
(2)B 酵母菌无氧呼吸产生的C02供给小球藻进行光合作用,乳酸菌无氧呼吸不产生C02?
(2013?盐城三模)如图,三棱锥P-ABC中,已知PA⊥平面ABC,△ABC是边长为2的正三角形,D,E分别为PB,PC
由静止开始释放,A球加速度的大小为B球的2倍.根据牛顿第二定律可知,A、B两个带电小球的质量之比为1:2;
当在AB中点固定一个带电小球C,由静止释放A、B两球,释放瞬间两球加速度大小相等,则有C球带正电,
根据库仑定律与牛顿第二定律,且有:对A来说,K
?K
=ma?
对B来说,K
+K
=2ma
综上解得,QC=
根据库仑定律与牛顿第二定律,且有:对A来说,
?
=ma
对B来说,k
+k
=2ma
综上解得,QC=
,故AB正确,CD错误;
故选:AB
(2014?盐城三模)如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为菱形,点F为侧棱PC上一点.(1)若PF=
(1)如图,取AC的中点F,连接BF,则BF⊥AC.以A为坐标原点,过A且与FB平行的直线为x轴,AC为y轴,AP为z轴建立空间直角坐标系,如图所示
则A(0,0,0),B(
,1,0),C(0,2,0),P(0,0,2),E(0,1,1)
∴
=(
,1,-2),
=(0,1,1)
设直线AE、PB所成的角为θ,则cosθ=|
|=
即直线AE与PB所成角的余弦值为
(2013?盐城三模)如图,一颗棋子从三棱柱的一个顶点沿棱移到相邻的另一个顶点的概率均为13,刚开始时,
解答:证明:(1)设AC,BD的交点为O,连OF,
∵底面ABCD为菱形,∴O为AC中点,
又PF=FC,∴PA∥OF,…(5分)
且PA?平面BDF,OF?平面BDF,
∴PA∥平面BDF.…(7分)
(2)∵底面ABCD为菱形,∴BD⊥AC,
∵PA⊥底面ABCD,∴BD⊥PA,∴BD⊥平面PAC,
∴BD⊥PC,
∵BF⊥PC,∴PC⊥平面BDF,
又PC?平面PBC,∴平面BDF⊥平面PBC.…(14分)
(2013?盐城三模)如图是7位评委给某作品打出的分数的茎叶图,那么这组数据的方差是______
(1)棋子在上底面点A处,若移了n次后,棋子落在上底面顶点,棋子从A出发.由3条路径,所以p1=
.
棋子移动两次,还在上底面时,有两种可能,p2=
×
+
(1?
)=
.
(2)因为移了n次后,棋子落在上底面顶点的概率为pn.
故落在下底面顶点的概率为1-pn.
于是,移了n+1次后,棋子落在上底面顶点的概率记为pn+1=
pn+
(1?pn)=
pn+
,从而pn+1-
=
(pn?
),
所以数列{pn?
}是等比数列,首项为
公比为
,所以pn?
=
×(
)n?1,
用数学归纳法证明:
>
.
①当n=1时左式=
=
,右式=
,因为
>
,所以不等式成立.
当n=2时,左式=
+
=
,右式=
,所以不等式成立;
②设n=k(k≥2)不等式成立,即
>
.
则n=k+1时,左式=
+
>
+
=
+
,
要证
+
≥
,
只要证
≥
?
,
即证:
≥
,
只要证
≤
,
只要证3k+1≥2k2+6k+2,
因为k≥2,所以3k+1=3(1+2)k≥3(1+2k+
)=6k2+3=2k2+6k+2+2k(2k-3)+1>2k2+6k+2
所以
+
≥
,
即n=k+1时不等式也成立,由①②可知
>
对任意n∈N*都成立.
由茎叶图知,七个数据为88,89,89,90,91,91,92,
平均数为?
=90;
方差为?
[(88-90)2+(89-90)2+(89-90)2+(90-90)2+(91-90)2+(91-90)2+(92-90)2]=
.
故答案为:
.