您现在的位置是: 首页 > 录取信息 录取信息
高考函数综合题及答案_高考函数综合
tamoadmin 2024-05-21 人已围观
简介第一步:因为f(X+2)=f(X-2), 可以得到f(x)=f(x-4),所以是以4为周期的函数。所以点(-5,f(-5))处切线的斜率就是点(-1,f(-1))处切线的斜率,即f‘(-5)=f‘(-1)。第二步:由f(x)是偶函数,由图形的对称性可以看出f‘(x)=-f’(-x),可以得到f‘(-1)=2.所以就得到f’(-5)=2.解:对任意x∈R,都满足f(x+1)=f(x-1) ∴f
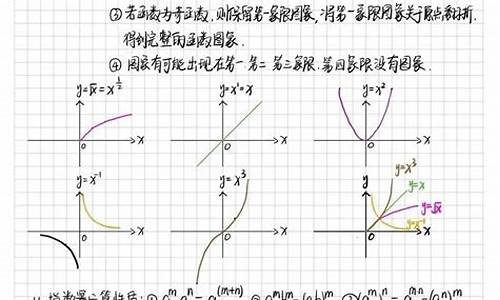
第一步:因为f(X+2)=f(X-2), 可以得到f(x)=f(x-4),所以是以4为周期的函数。所以点(-5,f(-5))处切线的斜率就是点(-1,f(-1))处切线的斜率,即f'(-5)=f'(-1)。
第二步:由f(x)是偶函数,由图形的对称性可以看出f‘(x)=-f’(-x),可以得到f‘(-1)=2.
所以就得到f’(-5)=2.
解:∵对任意x∈R,都满足f(x+1)=f(x-1)
∴f(x)=f(x+2)即f(x)是以2为最小正周期的周期函数,周期可表示为2K,K∈Z
∵f(1-x)=f(1+x)∴f(x)关于X=1对称
又当x∈[0,1]时,f(x)=x?-2x
∵f(x)=x?-2x关于X=1对称
∴x∈[1,2]时,f(x)=x?-2x,即是说当在函数的一个周期区间[0,2]上有
f(x)=x?-2x=(x-1)?-1
∴可以通过平移f(x)=x?-2x在x∈[0,2]的图像得到其他周期区间上的图像
向左平移2个单位得到在[-2,0]上的图像,其函数表达式为f(x)=(x-1+2)?-1=(x+1)?-1
从函数图像上易得到f(x)在[-1,1]上关于Y轴对称,∴f(x)在[-1,1]上是偶函数
最大值是0,最小值是-1,在[-1,0]上单调递增,在[0,1]上单调递减
当X=0时,f(x)=0,∴零点是X=0