高考四川数学文科数学_2021年四川高考文科数学难吗?

#高考# 导语2021年四川高考数学满分多少分？2021年高考即将来临，很多同学们和家长朋友们都想了解2021年四川的高考数学满分多少分。下面是由 为大家详细介绍一下，希望对大家有所帮助。

2021年四川高考数学满分多少分？

问：2021年四川高考数学满分多少分？

答： 四川仍将采用“3+文科”或“3+理科”的传统高考模式。即，语文、数学、外语+文科综合或语文、数学、外语+理科综合的模式。

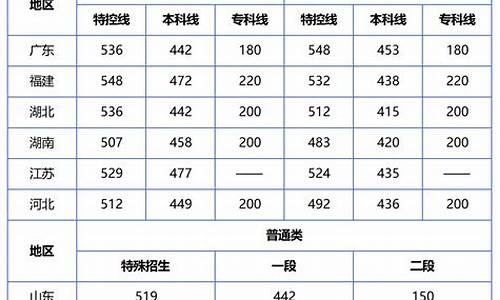
考总分均为750分。其中，语文、数学、外语满分均为150分，理科综合（物理、化学、生物）为300分；文科综合（政治、历史、地理）为300分。

新高考数学考试范围

　结合去年新高考数学全国一卷，我们可以总结出以下考试范围：

　①单项选择考试范围

　集合的基本运算、复数的基本运算、统计与概率-排列组合、立体几何、概率事件、指数与对数函数、平面向量与平面几何、函数的与导数。

　②多项选择考试范围

　解析几何(双曲线)、三角函数、不等式应用、对数运算及不等式基本性质。

　③填空题考试范围

　解析几何(抛物线)、数列(等差或等比)、三角函数、立体几何轨迹计算。

　④解答题考试范围

　三角函数(正弦余弦定理)、等比数列及其求和、统计与概率、立体几何、解析几何、函数与导数。

　通过对考试范围的分析，结合之前的分值统计，我们可以得出数学考点主要集中在以下几个方面：

如何快速提高高考数学成绩

　1、想提高数学成绩，首先要对自己的数学有一个整体的判断，比如自己在知识点上哪一块是优势，哪一块是需要弥补的地方。

　2、其次在发现自己薄弱处后，要在薄弱的知识点上下狠工夫，同样学习数学也需要一定的分类方法的，把一些关联的知识点结合起，做到关联学习，会事倍功半，避免盲目。但因为高中学科比较多，我们不可能每天都顾及到这门单一的学科，所以难免也会对数学的知识点有所遗忘。还有一个问题就是学生在给自己归类的时候可能会花费一些不必要的时间，这样的话我们就需要一个既节省时间又很智能的工具替我们维护这个效的学习方法。

　总体来说，学习数学就是三步：了解自己知识的优弱势；找出薄弱环节，归类并且不断强化；勤于练习，常复习。

提高数学成绩的技巧

　1.背例题

　这个是一个比较冷门但是效果奇好的提高数学成绩的方法。这个办法就是，遇到你不会的题目，如果怎么都做不出来，你就不用花时间弄懂它了，把它背下来，但是不要什么题都背，要背那种中等难度的题，高难的题一般以后也用不上，简单的你自己就会做。这样做一段时间，你会发现你节省了很多时间，遇到不会的题你也会往里面“套答案”了。

　2.课后复习

　高中数学一定要注意的一点就是时效性，一定要在课后及时复习，这样做的原因就是如果你隔几天在看，你会发现你的知识点已经忘记的差不多了，这个时候你在复习，就产不多相当于又重新在学一次，所以“趁热打铁”这个成语同样适用于高中数学的学习。其次，我们复习过得知识也不是一劳永逸的，每周、每个月都总结一下。这样有利于形成我们的知识网络，更加方便记忆。

高考考生注意事项

　进考场前要怎么调节心理

　在进入考试场之前，不要和同学有过多的接触，以免其中有人把紧张的情绪传染给你，在考试考试前半个小时左右可以听听音乐，放松一下。

　第一门考砸了怎么调整状态

　高考的考试科目是统一的，如果第一科是你的弱项，或者是没有考好，不要焦虑，也不要有压力，你要这样想，最不擅长的科目已经考完了，不需要担心下面的科目了。考完之后不要和同学对答案，那样会影响情绪，对下一科考试有不好的影响，要稳定情绪，调整状态，为下一科考试做准备。

　高考准考证丢了怎么办

　高考规定考生要带身份证和准考证入场，如果意外丢失或者忘带了，不要着急，经带队老师或有关证明确定是本考场的考生，警官主考官的批准，考生也可以先进入考场考试，同时考生要找人在考试之前把准考证取回或者补办，警官监考人员检查无误则本次考试才有效，否则本场考试是无效的。

　考前要调节情绪

　有很多同学在高考之前选择突击复习，这样使自己的大脑过度疲劳，加上紧张的情绪，在高考的考场上很容易发挥失常，所以，只要我们在高考之前进行了系统的复习，高考之前就不需要过度的去复习了，这个时候要做的就是尽量放松自己，保持一个愉悦的心态，迎接高考。

　考试之前要自信

　在面临高考的时候，很多的同学会会产生焦虑、紧张的情绪，其实我们完全不需要这样，我们要相信自己，用平常心去对待高考，高考并不一定会决定我们的人生，即使最不好的情况发生，我们还可以选择复读，所以我们要保持一个轻松，开心的状态，稳定住自己的情绪，发挥出自己的水平就可以了。

2011年普通高等学校招生全国统一考试

四川文数学解析

1.答案：B

解析：由M= {1,2,3,4,5}，N={2,4},则 N={1,2,3}.

2.答案：B

解析：大于或等于31.5的频数共有12+7+3=22个,所以P= = .

3.答案：D

解析：由 得 ,则圆心坐标是(2，-3).

4. 答案：A

解析：由函数 的图像关于直线y=x对称知其反函数是 ,故选A.

5.答案：A

解析：“x=3”是“x2=9”的充分而不必要的条件.

6.答案：B

解析：若 ， 则 , 有三种位置关系，可能平行、相交或异面，故A不对.虽然 ∥ ∥ ，或 ， ， 共点，但是 ， ， 可能共面，也可能不共面，故C、D也不正确.

7.答案：D

解析： = = = = .

8.答案：C

解析：由题意得 ,

, .

9.答案：A

解析：由a1=1, an+1 =3Sn(n ≥1)得a2=3=3×40,a3=12=3×41,a4=48=3×42,a5=3×43,a6=3×44.

10.答案：C

解析：由题意设当天派 辆甲型卡车， 辆乙型卡车，则利润 ，得约束条件 ,画出可行域在 的点 代入目标函数 .

11.答案：A

解析：横坐标为 ， 的两点的坐标 经过这两点的直线的斜率是 ,则设直线方程为 ，则 又 .

12.答案：B

解析：基本事件： .其中面积为2的平行四边形的个数 ；m=3故 .

13.答案：84

解析： 的展开式中 的系数是 =84.

14.答案：16

解析： ，点 显然在双曲线右支上，点 到左焦点的距离为20，所以

15.答案：

解析： 时， ，则 = .

16.答案：②③④

17. 本小题主要考查相互独立事件、互斥事件等概念及相关计算，考查运用所学知识和方法解决实际问题的能力．

解析 ：①中有 = ，但-2≠2,则①不正确；与“若 时总有 ”等价的命题是“若 时总有 ”故②③正确；函数f（x）在定义域上具有单调性的函数一定是单函数，则④正确.

解析：（Ⅰ）甲、乙在三小时以上且不超过四小时还车的概率的分别是 ， ，故甲、乙在三小时以上且不超过四小时还车的概率都是 .

（Ⅱ）设“甲、乙两人每次租车都不超过两小时”为事件A, “甲、乙两人每次租车一人不超过两小时，另一个人在两小时以上且不超过三小时还车”为事件B, 此时，所付的租车费用之和2元；“甲、乙两人每次租车都在两小时以上且不超过三小时还车”为事件C，此时，所付的租车费用之和4元；甲、乙两人每次租车一人不超过两小时，另一个人在三小时以上且不超过四小时还车”为事件D，此时，所付的租车费用之和4元；则 , , , .

因为事件A,B,C,D互斥，故甲、乙两人所付的租车费用之和小于6元的概率 .

所以甲、乙两人所付的租车费用之和小于6元的概率 .

18. 本小题考查三角函数的性质，同角三角函数的关系，两角和的正、余弦公式、诱导公式等基础知识和基本运算能力，函数与方程、化归与转化等数学思想．

解析：(Ⅰ)∵

（Ⅱ）由 ,

由 ,

两式相加得2 .

.

19.本小题主要考查直三棱柱的性质、线面关系、二面角等基本知识，并考查空间想象能力和逻辑推理能力，考查应用向量知识解决问题的能力．

解法一：

（Ⅰ）连结AB1与BA1交于点O，连结OD，

∵C1D∥AA1,A1C1=C1P, ∴AD=PD．

又AO=B10．∴OD∥PD1．

又OD 平面BDA1, PD1 平面BDA1.

∴PB1∥平面BDA1.

（Ⅱ）过A作AE⊥DA1于点E，连结BE．

∵BA⊥CA，BA⊥AA1，且AA1∩AC=A，∴BA⊥平面AA1C1C．

由三垂线定理可知BE⊥DA1．∴∠BEA为二面角A－A1D－B的平面角．

在Rt△A1C1D中， ，又 ，∴ ．

在Rt△BAE中， ，∴ ．

故二面角A－A1D－B的平面角的余弦值为 ．

解法二：

如图，以A1为原点，A1B1，A1C1，A1A所在直线分别为x轴，y轴，z轴建立空间直角坐标系A1－B1C1A，则 ， ， ， ．

（Ⅰ）在 PAA1中有设C1D＝ AA1，∵AC∥PC1，∴ ．由此可得 ，

∴ ， ， ．

设平面BA1D的一个法向量为 ，

则 令 ，则 ．

∵PB1∥平面BA1D，

∴ ，

∴PB1∥平面BDA1.

（Ⅱ）由（Ⅰ）知，平面BA1D的一个法向量 ．

又 为平面AA1D的一个法向量．∴ ．

故二面角A－A1D－B的平面角的余弦值为 ．

20. 本小题考查等比数列和等差数列的基础知识以及基本的运算能力，分析问题、解决问题的能力和化归与转化等数学思想．

解析：（Ⅰ）由已知, = ,∴ , ,

当 成等差数列时, 可得

化简得 解得 .

（Ⅱ）若 =1,则﹛ ﹜的每一项 = ,此时 ， ， 显然成等差数列.

若 ≠1, ， ， 成等差数列可得 + =2

即 + = 化简得 + = .

∴ + =

∴ ， ， 成等差数列.

21. 本小题主要考查直线、椭圆的标准方程及基本性质等基本知识，考查平面解析几何的思想方法及推理运算能力．

（Ⅰ）由已知得 ， ，所以 ，则椭圆方程为 ．

椭圆右焦点为( ,0),此时直线 的方程为 ,

代入椭圆方程化简得7 -8 =0.解得 =0, = ,

代入直线方程得 =1. =- .∴D点的坐标为

则线段 的长

（Ⅱ）直线 垂直于x轴时与题意不符．

设直线 的方程为 （ 且 ）．

代入椭圆方程化简得(4k2+1) -8k =0解得 =0, = ,

设代入直线 方程得 =1. = .∴D点的坐标为 ，

又直线AC的方程为： +y=1，直线BD的方程为： ，

联立解得 ,因此Q点的坐标为 ，又 ，

∴ ．

故 为定值．

22.本小题主要考查函数导数的应用、不等式的证明、解方程等基本知识，考查数形结合、函数与方程、分类与整合、特殊与一般等数学思想方法及推理运算、分析问题、解决问题的能力．

解：（Ⅰ）F(x)=18f(x)-x2[h(x)]2=-x3+12x+9( )

∴ -3x2+12，令 ，得 (x=-2舍)．

当 时， ；当 时， ．

故当 时， 是增函数； 时， 是减函数．

函数 在 处有得极大值 ．

（Ⅱ）原方程可化为 ，

①当 时，原方程有一解 ；

②当 时，原方程有二解 ；

③当 时，原方程有一解 ；

④当 或 时，原方程无解．

（Ⅲ）由已知得 ．

f(n)h(n)- = -

设数列 的前n项和为 ，且 （ ）

从而 ，当 时， ．

又

．

即对任意 时，有 ，又因为 ，

所以 ．

故 ．

故原不等式成立.