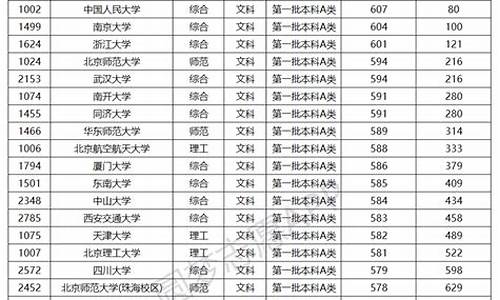
您现在的位置是: 首页 > 教育资讯 教育资讯
高考三角函数难题训练及答案_高考三角函数难题
tamoadmin 2024-06-09 人已围观
简介1.一道向量与三角函数结合的难题2.互为余角的日角三角函数关系三角函数的基本关系三角函数化简求值经典难题3.高中数学必修四任意角的三角函数难题!在线跪求!TAT详见照片!P为锐角三角形ABC内任一点,直线AP,BP,CP分别分别交三角形PBC,PCA,PAB的外接圆于另一点A1,B1,C1(不同于P),求证: (1+2*PA/PA1)*(1+2*PB/PB1)*(1+2*PC/PC1)>=8
1.一道向量与三角函数结合的难题
2.互为余角的日角三角函数关系三角函数的基本关系三角函数化简求值经典难题
3.高中数学必修四任意角的三角函数难题!在线跪求!TAT详见照片!
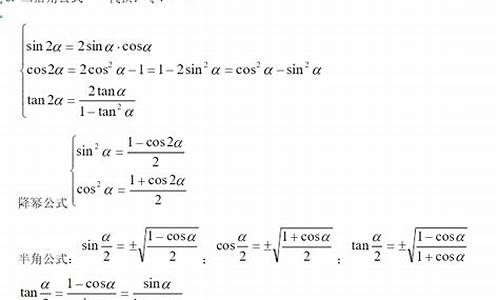
P为锐角三角形ABC内任一点,直线AP,BP,CP分别分别交三角形PBC,PCA,PAB的外接圆于另一点A1,B1,C1(不同于P),求证:
(1+2*PA/PA1)*(1+2*PB/PB1)*(1+2*PC/PC1)>=8
一道向量与三角函数结合的难题
题目错了一点地方!
应该是y=16-12cos?A-4cos?C ?(因为这里的自变量不是x)
解:
由根号3 cosA -cosC=1有3cos?A=(1+cosC)?
代入有:
y=16-4(1+cosC)? -4cos?C
=-8cos?C - 8cosC +12 ?, -8cosC∈(16-8根号3 ,16),故cosC∈(-4,根号3 -2)
令cosC=t,则t∈(-4,根号3 -2);
所以,
y=-8t? -8t +12 ,?t∈(-4,根号3 -2)
开口向下,对称轴为x= -1/2的抛物线在(-4,根号3 -2)的图像;
所以,y∈(-84,14为所求的值域!
互为余角的日角三角函数关系三角函数的基本关系三角函数化简求值经典难题
an=(cos nπ/7,sin nπ/7)
则a?n= cos ?nπ/7+sin? nπ/7=1,
ㄧbㄧ=1,
则b?=1.
y=ㄧa1+bㄧ?+ㄧa2+bㄧ?+ㄧa3+bㄧ?++ㄧa141+bㄧ?
=a?1+2a1b+ b?+ a?2+2a2b+ b?++ a?141+2a141b+ b?
=1+2a1b+1+1+2a2b+1+1+2a141b+1
=282+2(a1+a2+……+a141)b
cosπ/7+ cos2π/7+ cos2π/7+ cos2π/7+……+ cos7π/7+
cos8π/7+ cos9π/7+ cos10π/7+ cos11π/7+……+ cos14π/7
= cosπ/7+ cos2π/7+ cos2π/7+ cos2π/7+……+ cos7π/7
-cosπ/7-cos2π/7- cos3π/7- cos4π/7+……- cos7π/7
=0,
sinπ/7+ sin2π/7+ sin2π/7+ sin2π/7+……+ sin7π/7+
sin8π/7+ sin9π/7+ sin10π/7+ sin11π/7+……+ sin14π/7
= sinπ/7+ sin2π/7+ sin2π/7+ sin2π/7+……+ sin7π/7
-sinπ/7-sin2π/7- sin3π/7- sin4π/7+……- sin7π/7
=0,
因为cos nπ/7与sin nπ/7的周期都是14,
所以a1+a2+……+a141=a1
(a1+a2+……+a141)b=a1b≤|a1||b|=1
∴y=282+2(a1+a2+……+a141)b
≤282+2=284.
高中数学必修四任意角的三角函数难题!在线跪求!TAT详见照片!
(1)一次齐次时,分子分母同时除以cosa,就行了。 (2)因为(cosa)^2+(sina)^2=1 这个题是二次齐次式,整体除以(cosa)^2+(sina)^2 得[2(sina)^2-3sinacosa-2(cosa)^2]/[(cosa)^2+(sina)^2] 分子分母同时除以(cosa)^2 得[2(tana)^2...
(1) y=1/(sinxcosx)=2/sin2x
sin2x≠0
2x≠kπ
则 x≠kπ/2
(2) y=tanx/(1+sinx)
1+sinx≠0 和x≠π/2+kπ
sinx≠-1
x≠3π/2+2kπ
故 x≠π/2+kπ
(2) -cosα<0
{α| π/2<α<3π/2}∪ {α| -3π/2<α< -π/2}