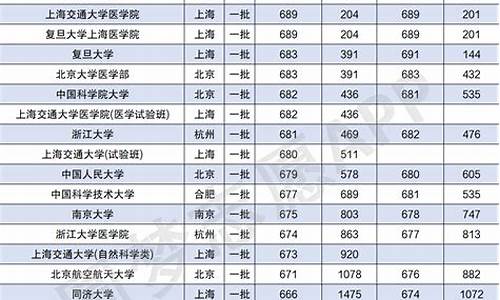
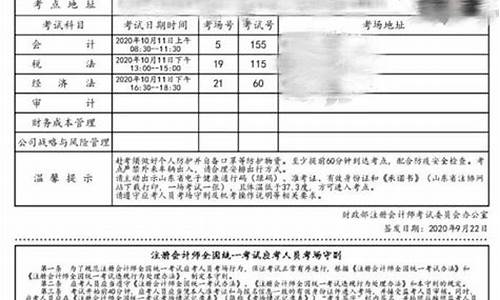
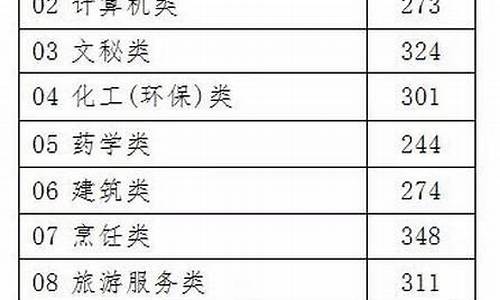
您现在的位置是: 首页 > 教育改革 教育改革
高考函数真题,高考函数真题汇编以及解析
tamoadmin 2024-06-05 人已围观
简介1.很难很那数学题!?已知定义在R上的奇函数f(x)满足f(x)=-f(x-2)2.求10道高中数学函数类型的题目3.高考摸题--函数解:f(x)=3sinwx+coswx=2sin(wx+π/6)该函数图像与直线y=2的两个相邻交点的距离等于π∴该函数周期T=π=2π/w∴w=2∴f(x)=2sin(2x+π/6)令-π/2+2kπ2x+π/6π/2+2kπk∈Z得:kπ-π/32x+π/6kπ
1.很难很那数学题!?已知定义在R上的奇函数f(x)满足f(x)=-f(x-2)
2.求10道高中数学函数类型的题目
3.高考摸题--函数
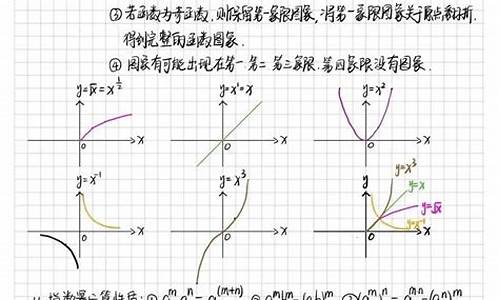
解:f(x)=√3sinwx+coswx=2sin(wx+π/6)
∵该函数图像与直线y=2的两个相邻交点的距离等于π
∴该函数周期T=π=2π/w
∴w=2
∴f(x)=2sin(2x+π/6)
令-π/2+2kπ≤2x+π/6≤π/2+2kπ
k∈Z
得:kπ-π/3≤2x+π/6≤kπ+π/6
k∈Z
答案应该为C
很难很那数学题!?已知定义在R上的奇函数f(x)满足f(x)=-f(x-2)
因为cosα =3/5 且 0<α<(2/π)
所以sinα =4/5
又 sin(α+β)=sinα cosβ +cosα sinβ (和差化积)
sinβ等于根号下1减cosβ的平方
带入即可解得cosβ
求10道高中数学函数类型的题目
此题是2009年山东高考试题(理科)第16题,原题是这样子:
已知定义在R上的奇函数f(x)满足f(x)=-f(x-4),且在区间0,2上为增函数,若方程f(x)=m(m>0)在区间-8,8上有四个不同的根X1
X2
X3
X4,则X1+X2+X3+X4
=?
解定义在R上的奇函数f(x)满足f(x)=-f(x-4),
所以f(x)=
f(4-x),函数图像关于直线x=2对称且f(0)=0.
由f(x-4)
=-
f(x)可知:f(x-8)
=f(x),函数周期为8.
又因函数在区间0,4上为增函数,所以函数在-4,0上也是增函数。
根据以上分析可以画出函数图像的简图。
方程f(x)=m(m>0)在区间-8,8上有四个不同的根X1,X2,X3,X4,
不妨设X1<X2<X3<X4,由对称性可知:X1+X2=-12,X3+X4=4,所以X1+X2+X3+X4=-8.
高考摸题--函数
1,若x是方程lgx+x=2的解,求x属于的区间。 2,把函数y=lg(2x)的图像a平移,得到函数y=lg(x-1)的图像,求a. 3,设函数f(x)=cos(x的绝对值+30度)(x是实数),求函数单调区间。 4,若函数f(x)=(X^2+bx+c)e^-x在(负无穷,-1),(1,正无穷)上单调递减,在(-1,1)单调递增,求b+c的值。 5,画出函数y=(2^x+1)\(2^x-1)的大致图像。 6,依次画出3^x,3^x+1,3^(x+1),3^x的绝对值的图像, 7,sin(x)经怎样变换得Asin(wx+b)+c,请用两种方法说明。 8,(ax+b)\(cx+d)的图像的中心对称点及变换方式。 9,f(x)图像关于原点坐标对称的图像恰好为y=3-2x的图像,求f(x). 10,e^x按照向量a=(2,3)平移得到新函数g(x),求g(x). 只是些容易题 ,做好这些,你就可以去做高考题啦!(结果如何,概不负责)但还是给点分额吧!
已知函数f(x)=ln[e^x+a](a为常数)是实数集R上的奇函数,
函数g(x)=λf(x)+sinx是区间[-1,1]上的减函数。
(1)求a的值。
(2)若g(x)≤t?+λt+1在x∈[-1,1]上恒成立,求t的取值范围。
(3)讨论关于x的方程(lnx)/f(x)=x?-2ex+m的根的个数。
(1)f(x)是奇函数--->f(0)=0,即ln(1+a)=0--->a=0
(2)--->f(x)=x--->g(x)=λx+sinx是区间[-1,1]上的减函数
--->g'(x)=λ+cosx≤0在区间[-1,1]上恒成立--->λ≤-1
--->g(x)=λx+sinx在[-1,1]上的最大值=g(-1)=-(λ+sin1)
g(x)≤t?+λt+1在x∈[-1,1]上恒成立即:g(-1)≤t?+λt+1成立
--->t?+λt+(1+λ+sin1)≥0--->λ(t+1)≥-(t?+1+sin1)
∵λ≤-1,∴(t+1)<0且-(t?+1+sin1)/(t+1)≥-1
--->t?+1+sin1≥t+1--->t?-t+sin1≥0,
Δ<0显然成立
--->t<-1
(3)(lnx)/f(x)=x?-2ex+m
下一篇:四川俄语高考平均分_四川俄语高考