数学函数高考真题_数学函数高考题

1.问一题关于函数的数学题``后天就要高考嘞``

2.数学辅导：求函数解析式的几种常用方法

3.急！怎么做对高考数学三角函数大题！

4.高考数学问题:若函数f(x)=ax

5.高考数学16题求帮忙 已知函数f(x)=2cos^2wx+sin2wx(w>0)的相邻两对称轴

6.一道高中数学函数题 快高考了谢谢大家~

高考数学基础题二次函数、复合函数。?

1、二次函数。

二次函数解析式的三种形式：

一般式：f（x）＝ax2＋bx＋c（a≠0）。

顶点式：f（x）＝a（x－m）2＋n（a≠0）。

零点式：f（x）＝a（x－x1）（x－x2）（a≠0）。

辨明两个易误点：

对于函数y＝ax2＋bx＋c，要认为它是二次函数，就必须满足a≠0，当题目条件中未说明a≠0时，就要讨论a＝0和a≠0两种情况。

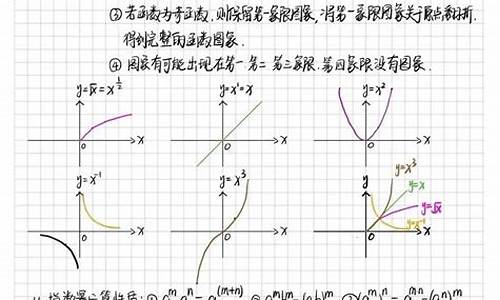
幂函数的图象一定会出现在第一象限内，一定不会出现在第四象限内，至于是否出现在第二、三象限内，要看函数的奇偶性；幂函数的图象最多只能同时出现在两个象限内；如果幂函数图象与坐标轴相交，则交点一定是原点。

2、复合函数。

设函数Y=f（u）的定义域为D，函数u=φ（x）的值域为Z，如果D∩Z，则y通过u构成x的函数，称为x的复合函数，记作Y=f（φ（x））。

x为自变量，y为因变量，而u称为中间变量。? 如等都是复合函数。? 就不是复合函数，因为任何x都不能使y有意义。由此可见，不是任何两个函数放在一起都能构成一个复合函数。

高考数学必备技巧：

1、三个“基本”：基本的概念要清楚，基本的规律要熟悉，基本的方法要熟练。

2、做完题目后一定要认真总结，做到举一反三，这样，以后遇到同一类的问题是就不会花费太多的时间和精力了。

3、一定要全面了解数学概念，不能以偏概全。

4、学习概念的最终目的是能运用概念来解决具体问题，因此，要主动运用所学的数学概念来分析，解决有关的数学问题。

5、要掌握各种题型的解题方法，在练习中有意识的地去总结，慢慢地培养适合自己的分析习惯。

6、要主动提高综合分析问题的能力，借助文字阅读去分析理解。

7、在学习中，要有意识地注意知识的迁移，培养解决问题的能力。

8、要将所学知识贯穿在一起形成系统，我们可以运用类比联系法。

9、将各章节中的内容互相联系，不同章节之间互相类比，真正将前后知识融会贯通，连为一体，这样能帮助我们系统深刻地理解知识体系和内容。

10、在数学学习中可以利用口诀将相近的概念或规律进行比较，搞清楚它们的相同点，区别和联系，从而加深理解和记忆。弄清数学知识间的相互联系，透彻理解概念，知道其推导过程，使知识条理化，系统化。

问一题关于函数的数学题``后天就要高考嘞``

1.当x>=0时,f(x)=2^x-1/2^x,令2^x=a(a>0),那么既

a-1/a=2.解得a=1+根号2,此时X=log(2)(1+根号2)

当x<0时,f(x)=2^x-2^x=0(无解)

综上x=log(2)(1+根号2)

2.当t属于[1.2]时,f(t)属于[3/2,15/4]

对不等式移项得.mf(t)>=

-2^f(2x)要恒成立

又因为

f(2x)属于R,所以2^f(2x)>0

所以

(1)显然当m>=0时不等式成立

(2)当m<0时,只要m>=

-2^f(2x)/f(t)恒成立,既m>=max{-2^f(2x)/f(t)}

而后面哪个式子的极限是0,所以m>=0就可以了,与m<0矛盾(舍去)

总之,m>=0

数学辅导：求函数解析式的几种常用方法

由于f是偶函数，所以在y轴两侧对称；

由于f(1/3)=0且f在正轴上递增，所以f在（-1/3，1/3）上小于0；

由上面的分析，我们要求x满足：

1，使log1/8 X有意义，即x〉0；

2，使log1/8 X大于1/3或者小于-1/3.

再注意到log1/8 X关于x单调减少，于是x的取值范围是

0<x<(1/8)^(1/3)=1/2,或者

x>(1/8)^(-1/3)=2

整理可得：（0，1/2）并上（2,正无穷）

急！怎么做对高考数学三角函数大题！

当前，我们已进入高三一轮复习，函数是高中数学的核心内容，也是学习高等数学的基础，是数学中最重要的概念之一，它贯穿中学数学的始终。求函数解析式是函数部分的基础，在高考试题中多以选择、填空形式出现，属中低档题目，同学们务必要拿分。下面就向同学们介绍几种求函数解析式的常用方法：

[题型一]配凑法

例1.已知f(■+1)=x+2■，求f(x)。

分析：函数的解析式y=f(x)是自变量x确定y值的关系式，其实质是对应法则f：x→y，因此解决这类问题的关键是弄清对“x”而言，“y”是怎样的规律。

解：∵f(■+1)=x+2■=(■+1)2-1

(■+11)

∴f(x)=x2-1(x1)

小结：此种解法为配凑法，通过观察、分析，将右端“x+2■”变为接受对象“■+1”的表达式，即变为含(■+1)的表达式，这种解法对变形能力、观察能力有一定的要求。

[题型二]换元法

例2.已知f(1-cosx)=sin2x，求f(x)。

分析：视1-cosx为一整体，应用数学的整体化思想，换元即得。

解：设t=1-cosx

∵-1cosx1 ∴01-cosx2 即0t2

∴cosx=1-t

∴sin2x=1-cos2x=1-(1-t)2=-t2+2t

∴f(t)=-t2+2t(0t2)

即f(x)=-x2+2x(0x2)

小结：①已知f[g(x)]是关于x的函数，即f[g(x)]=F(x)，求f(x)的解析式，通常令g(x)=t，由此能解出x=(t)，将x=(t)代入f[g(x)]=F(x)中，求得f(t)的解析式，再用x替换t，便得f(x)的解析式。

注意：换元后要确定新元t的取值范围。

②换元法就是通过引入一个或几个新的变量来替换原来的某些变量的解题方法，它的基本功能是：化难为易、化繁为简，以快速实现未知向已知的转换，从而达到顺利解题的目的。常见的换元法是多种多样的，如局部换元、整体换元、三角换元、分母换元等，它的应用极为广泛。

[题型三]待定系数法

例3.设二次函数f(x)满足f(x+2)=f(2-x)，且f(x)＝0的两实根平方和为10，图象过点(0，3)，求f(x)的解析式。

分析：由于f(x)是二次函数，其解析式的基本结构已定，可用待定系数法处理。

解：设f(x)＝ax2+bx+c(a≠0)

由f(x+2)=f(2-x)可知，该函数图象关于直线x=2对称

∴-■=2，即b=-4a……①

又图象过点(0，3) ∴c=3……②

由方程f(x)=0的两实根平方和为10，得(-■)2-■=0

即b2-2ac=10a2……③

由①②③解得a=1，b=-4，c=3

∴f(x)=x2-4x+3

小结：我们只要明确所求函数解析式的类型，便可设出其函数解析式，设法求出其系数即可得到结果。类似的已知f(x)为一次函数时，可设f(x)=ax+b(a≠0)；f(x)为反比例函数时，可设f(x)=■(k≠0)；f(x)为二次函数时，根据条件可设

①一般式：f(x)=ax2+bx+c(a≠0)

②顶点式：f(x)=a(x-h)2+k(a≠0)

③双根式：f(x)=a(x-x1)(x-x2)(a≠0)

[题型四]消元法

例4.已知函数y=f(x)满足af(x)+bf(■)=cx，其中a、b、c都是非零常数，a≠±b，求函数y=f(x)的解析式。

分析：求函数y=f(x)的解析式，由已知条件知必须消去f(■)，不难想到再寻找一个方程，构成方程组，消去f(■)得f(x)。如何构成呢？充分利用x和■的倒数关系，用■去替换已知中的x便可得到另一个方程。

解：在已知等式中，将x换成■，得af(■)+bf(x)=■，把它与原条件式联立，得af(x)+bf(■)=cx……①af(■)+bf(x)=■……②

①×a-②×b得(a2-b2)f(x)=c(ax-■)

∵a≠±b ∴f(x)=■(ax-■)(x≠0)

(周六继续刊登)

有同学通过QQ询问下面的数学题，我们请天津四中的孟黎辉老师来回答。

问1.已知：方程：x2+ax+a+1=0的两根满足一个条件：一根大于k，一根小于k(k是实数)，求a的取值范围。(此题一种方法是图象法，还有一种方法，能告诉这两种方法吗？)

答：方法一：∵f(x)=x2+ax+a+1图象为开口向上的抛物线，因此只需f(k)＜0即可。

∴k2+ak+a+1＜0，即a(k+1)＜-k2-1

∴当k＞-1时，a＜■；当k＜-1时，a＞■；当k=-1时，a无解。

方法二：(x1-k)(x2-k)＜0△＞0

只需(x1-k)(x2-k)＜0即可，x1x2-k(x1+x2)+k2＜0

即a+1+ka+k2＜0，以下同方法一。

问2.为什么求解时只需求(x1-k)(x2-k)＜0，而不需再求根的判别式是否大于0？

答：法二不需要验判别式，原因可以举个简单例子说明，如：若研究x2+ax+b=0两根满足：一个根大于0，一个根小于0，只需x1x2＜0，即：b<0，此时就可以保证△=a2-4b＞0恒成立。

高考数学问题:若函数f(x)=ax

三角函数最重要的公式：(sinX)^2+(cosX)^2=1

tanX=sinX/cosX

诱导公式六个，每个里面含sin，cos，tan各一个，总共18个。

角的和差公式，sin(a±b)=sina.cosb±cosa.sinb

cos(a±b)=cosa.cosb干sina.sinb

tan(a±b)=(tana±tanb）/1干tana.tanb

二倍角公式：sin2x=2sinX.cosX

cos2x=(cosX)^2-(sinX)^2=(cosX)^2-1=1-(sinX)^2

tan2x=2tanX/1-(tanX)^2

三角函数的题基本上就是以上公式反复换用，基本要记住特殊角的各个三角函数，30度、60度、45度等

高考数学16题求帮忙 已知函数f(x)=2cos^2wx+sin2wx(w>0)的相邻两对称轴

D

若a>1，则f(x)在[-2,2]上单调递增，只需a^2<2即可，解得a<根2，所以1<a<根2。

若0<a<1,则只需a^-2<2即可，解得a>（根2)/2.

综上，选D

a^2是a的2次方。

此类问题用“大于最大的，小于最小的”原理。

一道高中数学函数题 快高考了谢谢大家~

f(x)=2cos^2wx+sin2wx(w>0)

=1+cos2wx+sin2wx

=1+√2sin(2wx+π/4)

∵相邻两对称轴的距离为派/2

∴T/2=π/2,T=π, 2π/(2w)=π

∴w=1

2

f(x)向下平移一个单位得

g(x)=√2sin(2x+π/4)

∵x∈[0,派/2]

∴2x+π/4∈[π/4,5π/4]

∴2x+π/4=5π/4,g(x)min=-1

2x+π/4=π/2,g(x)max=√2

g(x)在[0,派/2]上的取值范围是[-1,√2]

令x=tant，则y（t）=m*sint*2+4*3^1/2*sint+n*cos^2，用二倍角公式化简，y（t）=2*3^1/2sin2t+(n-m)/2*cos2t+(n+m)/2=(12+((n-m)/2)^2)^1/2*sin(2t+a)+(n+m)/2，y(t)max=(12+((n-m)/2)^2)^1/2+(n+m)/2=7，y(t)min=—(12+((n-m)/2)^2)*1/2+(n+m)/2=—1，m=1，n=5或m=5，n=1。